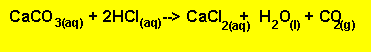Chemistry- volumetric analysis backtitration

A typical back titration involves the deliberate addition of excess reagent. Here we add the impure sample of limestone (calcium carbonate) to excess HCl. The reaction proceeds according to the equation below. The excess amount of HCl can be determined very accurately.

Next step is to now titrate the solution with a base to determine how much acid remained unreacted. This way we can work out exactly how much acid did react. We can then use stoichiometry to determine the amount of calcium carbonate present.

Click to hide this information

We titrate the solution with a known sodium carbonate solution of accurately known concentration.

The reaction takes place according to the equation above. A suitable indicator is used to give a colour change at the end point.

Click to hide this information

Solution

Step 1 - Work out the equations for all the reactions taking place.

The equation for the reaction between HCl with the limestone is given below.
Equation 1

The equation for the reaction between HCl and sodium carbonate is given below.
Equation 2

Step 2 - From equation 2 we can work out the mole of HCl left unreacted.

Step 3 - Work out how much HCl did react. Subtract the amount in excess from the amount originally added.

Amount originally added - amount in excess = amount reacted.
(0.1 X 1.1) - 0.0602 = 0.0498 mole of HCl reacted.

Step 3 - Using equation 1 calculate the amount of caclium carbonate present.
Mole of HCl /2 = mole of calcium carbonate = 0.0498/2 = 0.0249 mole.

Step 4 - Calculate the mass of calcium carbonate present.

0.0249 X formula mass = 0.0249 X 100 = 2.49 grams

Step 4 Calculate the percentage
2.49/3.00 X100 = 83.0%

Click to hide the solution

Volumetric analysis

Backtitration

This technique involves the deliberate addition of excess reagent to the test sample. After the reaction is complete the amount in excess is then determined by titration.

A feature of this technique is that we use excess reagent and two stoichiometric equations.We generally use this technique when we are dealing with very weak acids and bases that are unable to make an indicator change colour sharply at the end point of a titration.
Lets see an example, although in this example we are using a strong acid it is just the process that we are concerned about.

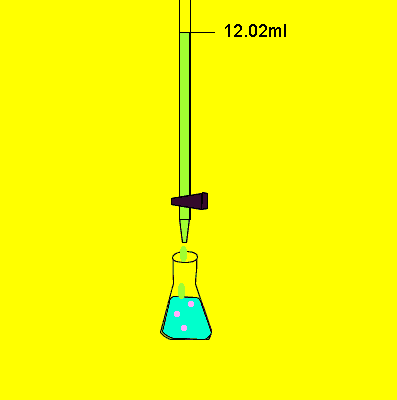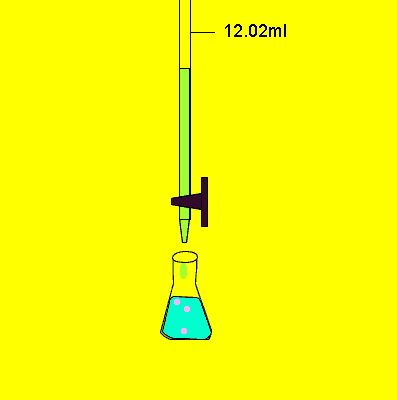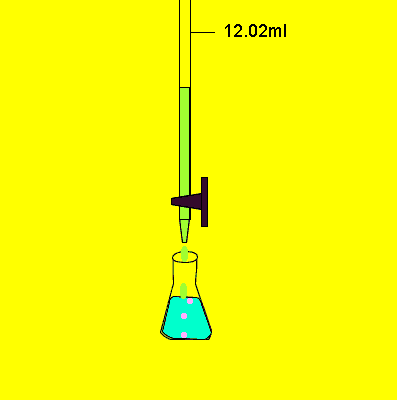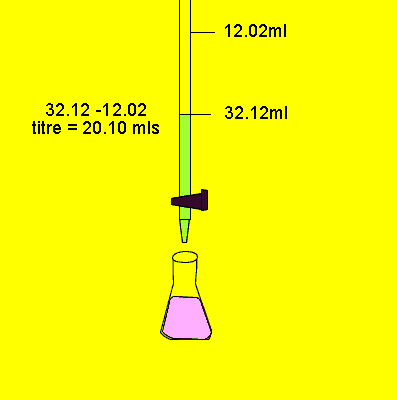
A 20.0g piece of steel wool is dissolved in 300.0mL of 1.00M sulphuric acid, H₂SO₄. The excess sulphuric acid is determined by titration with a 0.500M NaOH solution, as shown on the right. 280.0mL of sodium hydroxide is required to neutralise the acid. What was the percentage, by mass, of iron in the steel wool?

Step 1) Find the mole of NaOH used to neutralise the excess acid.
(n = c v) 0.500 x 0.280 = 0.140

Step 2 Derive the equation of the reaction between NaOH and H₂SO₄.

2NaOH_(aq) + H₂SO_4(aq) => Na₂SO_4(aq) + 2H₂O_(l)

Step 3 From the equation above find the excess H₂SO₄.
(n=cv) ½ x 0.140 = 0.0700

Step 4 Calculate the initial amount of H₂SO₄.used
(n=cv) 1.00 x 0.300 = 0.300

Step 5 Calculate the amount of H₂SO₄ that reacted.
0.300 – 0.0700 = 0.230

Step 6 Derive the equation for the reaction between H₂SO₄ and Fe

Fe(s) + H₂SO₄.(aq) => FeSO_4(aq) + H_2(g)

Step 7 Calculate the mol of Fe in steel wool 1/1 x 0.230 =0.230

Step 8 Calculate the mass of Fe (m=n x Fm) 0.230 x 55.8 = 12.83g

Step 9 Calculate the % of Fe (12.83 / 20.0) x 100/1 = 64.2%

3.00g sample of impure limestone is treated with 100ml of 1.1M HCl solution. The reaction takes place according to the equation below.

CaCO_3(aq) + 2HCl_(aq) => CaCl_2(aq) + H₂O_(l) + CO_2(g)

After the reaction is complete it is found that 20.10mls of a 1.50M sodium carbonate solution is required to neutralise the unreacted acid.

Calculate the percentage of calcium carbonate in the sample.

(Ca = 40.0, C= 12.0, O=16.0, CL =35.5, H =1.0)

	Volume
Start	12.02mls
Finish	32.12 mls
Total	*20.10mls*

Solution

Continue with another exercise

Home