Since the temperature, pressure and volume of each gas changes but the amount remains fixed, use the formula below.
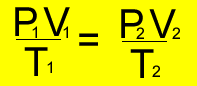
and tranform to make it equal
to P2
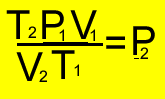
More clues
Hide the clues
Hide the clues
Step
1 Use the appropriate formula
to calculate the pressure of each gas, as if it was on its own, in the 60L
vessel.
Step 2 Add
up the individual pressures of each gas
Hide
P1V1
= P2V2
Continue
with assistance.
P1V1 = P2V2
For oxygen
P1 = 120 kPa, V1 = 25L, P2 = ?, V2 = 60L,
P2 = (120 X 25)/60 = 50 kPa.
For gas nitrogen
P1 = 200 kPa, V1 = 25L, P2 = ?, V2 = 60L,
P2 = (200 X 25)/600 = 83.3 kPa.
Hide the solution
Since the temperature, pressure and volume of each gas changes but the amount remains fixed, use the formula below.
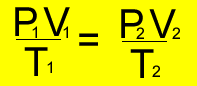
and tranform to make it equal
to P2
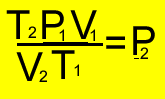
More clues
Hide the clues
Hide the clues
Calculating the partial pressure of oxygen where
P1 =230 kPa
V1 = 40L
T1 = (20 + 273) = 293K
T2 = (100 + 273) =373K
V2 = 100L
P2 = 230 X 40 X 373/(293 X 100) = 117.12 kPa
Calculating the partial pressure of hydrogen where
P1 =100 kPa
V1 = 60L
T1 = (20 + 273) = 293K
T2 = (100 + 273) =373K
V2 = 100L
P2 = 100 X 60 X 373/(293 X 100) = 76 38 kPa
|
Partial pressure (Dalton's Law)
|
|
|
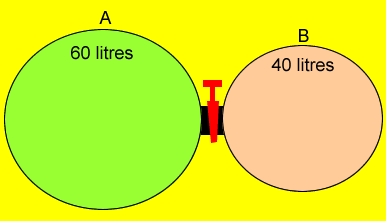
Two containers are connected by a stopcock as shown on the left. Gas "A" is at a pressure of 202 kPa while gas "B" is at a pressure of 140 kPa. What will the resultant pressure be when the stopcock is opened? Step 1 Calculate the pressure
that each gas alone will exert when the stopcock is opened. P1V1 = P2V2
|
|
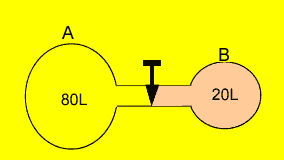
Two containers
are connected by a stopcock as shown on the right. Gas "A" is
at a pressure of 402 kPa while gas "B" is at a pressure of 100
kPa. What will the resultant pressure be when the stopcock is opened?
|
 |
|
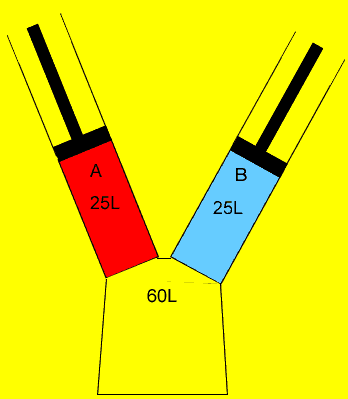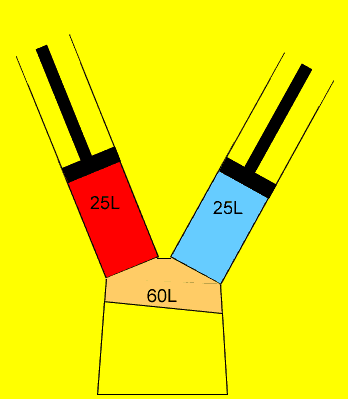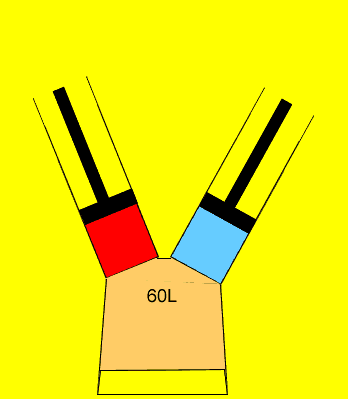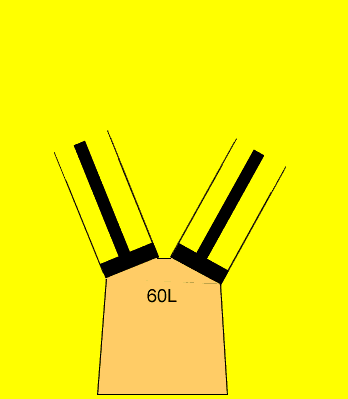
25 litres of oxygen gas at 120kPa and 25 litres of nitrogen gas at 200 kPa are pumped into an evacuated(empty) 60 litre vessel. What is the final pressure of the 60 litre vessel if the temperature remained constant? Clues |
 |
|
An 60 litre metal vessel contains carbon dioxide at 160 kPa and 23oC. A further 300 litres of nitrogen gas are pumped into this vessel at 140 kPa and 23oC. If the volume of the vessel and temperature remain constant what is the final pressure of the vessel?
|
|
|
A vessel containing 60L of
hydrogen gas at 20oC and 100kPa pressure is connected via a
valve to a 40L vessel containing oxygen at 20oC and 230kPa
pressure. The valve is opened and both gases expand to fill the entire
volume of both vessels. Answer |
 |