Relationship between temperature, volume and pressure
for a fixed amount of gas
Combining Charles' and Boyle's Laws we get the expression on the right. In keeping with the SI units
V = volume in litres
T = temperature in kelvin
P = pressure in kPa. Although units are not critical we will stick to using kPa.
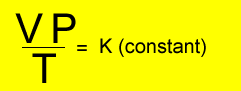
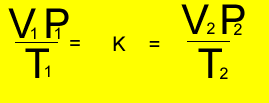
Changing the temperature, pressure and volume of a fixed amount of gas the expression on the left is true. Where P1 is the initial pressure and P2 is the final pressure and so on.
So let's put it to good use and see how it all works by trying some exercises below.

A fixed amount of gas was placed in a 6 litre vessel at 440 kPa at 30oC . The vessel was left in the heat and allowed to expand to 10.5 litres at a pressure of 490 kPa. What is the temperature of the gas?
Step 1 Select the appropriate formula
Step 2 Transform the formula to make it equal to temperature (T2)
Step 3 Replace the pronumerals on the right of the equation with their respective values and solve for temperature.
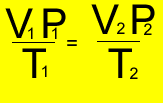
V1 = 6 L
T1 = (30 + 273 ) = 303K
P1 = 440 kPa
V2 = 10.5 L
P2 = 490 kPa
T2 = ?oK

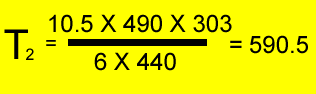
1) A fixed amount of gas is placed in a 2.5 litre vessel at 20oC and 95 kPa. The same gas is transferred into a 2 litre vessel at a temperature of 40oC . What is the pressure exerted by the gas?
Solution

2) 400 ml of pure hydrogen gas was collected at 27oC and 90.5 kPa. It was later transferred into a 20 ml container at a temperature of -20oC. What is the pressure of the gas?
3) One of the tyres of a car has a volume of 45 litres. The driver pumps the tyres up to a pressure of 320 kPa at 17oC. After a long drive the temperature of the tyres increased to 27oC . The tyre manufacturer recommends that the tyres not be inflated beyond 400 kPa as a blow out is likley to occur. Is the driver in danger of having a blow out?